Многопараметрическая оптимизация
При решении
исследовательских задач связанных с поиском
рационального сочетания сразу нескольких
параметров двигателя, таких как степень сжатия,
опережение впрыска, диаметр, число и
направленность сопел распылителя, форма камеры
сгорания, интенсивность вихря, фазы
газораспределения, параметры турбонаддува и др.
зачастую бывает трудно спланировать и
обработать численный эксперимент с большим
количеством варьируемых факторов. В этом случае
очень эффективным средством является
многопараметрическая оптимизация, когда поиск
рационального сочетания варьируемых факторов
возлагается на формальную процедуру нелинейного
программирования, а исследователю остается
только грамотно сформулировать задачу
оптимального поиска и проанализировать
полученное решение.
Целевая функция:
Показатели эффективности двигателя
или отдельных его процессов могут быть включены
в целевую функцию:
Zj = Zj (Xk).
Нахождение экстремума целевой функции является
задачей оптимизации.
Вектор независимых переменных:
Набор конструктивных параметров
двигателя, за счет выбора величины которых
планируется достичь экстремума целевой функции
составляет вектор независимых переменных Xk .
Ограничения:
Как правило при поиске
оптимального сочетания конструктивных
параметров двигателя необходимо контролировать
его тепловую и механическую напряженность,
также уровень эмиссии вредных веществ и другие
контрольные факторы которые ограничивают
область оптимального поиска и являются
ограничениями. Ограничительные параметры,
также как и целевая функция зависят от
независимых переменных Yi = Yi (Xk).
Аналитической связи между
целевой функцией и ограничениями с одной стороны
и вектором независимых перменных с другой
стороны не существует, поэтому для их вычисления
используется математическая модель
комбинированного ДВС.
Таким образом, задача оптимизации
процессов в ДВС сводится к задаче нелинейного
программирования, т.е. отыскания оптимума
функции многих переменных Zj при
выполнении условий (ограничений): Yi min < Yi
< Y i max. Наличие ограничений
существенно усложняет решение оптимизационных
задач, поэтому целесообразно свести задачу
условной оптимизации к задаче безусловной
оптимизации, алгоритмы для которой гораздо лучше
разработаны. Эффективным способом учета
ограничений является метод штрафных функций.
Суть метода состоит в том, что к минимизируемой
целевой функции добавляются штрафы,
возрастающие при нарушении ограничений. В общем
случае минимизируемая функция, с которой
работает поисковая процедура безусловной
оптимизации имеет вид:
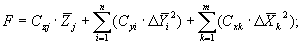
где: Czj
-
коэффициент влияния оптимизируемого параметра Zj;
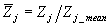
|
- оптимизируемый параметр Zj,
отнесенный к своему среднему значению; |
Cyi |
- коэффициент штрафа накладываемого на
целевую функцию при выходе нарушении
ограничения Yi; |
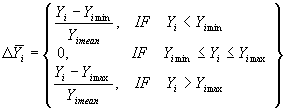 |
 -
относительная величина нарушения
ограничения Yi; |
Cxk
|
- коэффициент штрафа, накладываемого на
целевую функцию при выходе независимой
переменной Xk за пределы области допустимых
значений; |
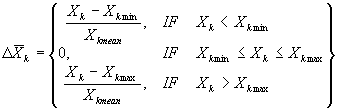 |
- относительная величина выхода независимой
переменной Xk за пределы области допустимых
значений; |
Средние значения независимых
переменных и величин ограничений вычисляются
программно как средние арифметические от
максимального и минимального значений.
Коэффициенты влияния
оптимизируемых параметров устанавливаются
программой автоматически.
Выбор коэффициентов штрафа,
максимальных и минимальных значений
параметров оптимизации Xk и ограничений Yi,
а также выбор показателя двигателя, который
будет использоваться как целевая функция Zj
осуществляется пользователем в оболочке
программного комплекса ДИЗЕЛЬ-РК, путем
заполнения соответствующих таблиц .
Библиотека алгоритмов программного
комплекса ДИЗЕЛЬ-РК .
Для поиска экстремума функции
многих переменных F могут быть
использованы различные процедуры из библиотеки
комплекса, содержащей 14 поисковых методов.
Большое количество методов необходимо для
проверки полученных решений. Если решение задачи
разными методами приводит к одному и тому же
результату, то можно с большей уверенностью
утверждать что полученное решение действительно
оптимально.
Подробно ознакомиться с
используемыми в комплексе ДИЗЕЛЬ-РК алгоритмами
оптимального поиска можно в следующих
публикациях :
- Химмельблау Д. Прикладное нелинейное
программирование.- М.:Мир, 1975.-535 с.
- Численные методы условной оптимизации /
М.Дж.Д.Пауэлл, Ф.Гилл, У.Мюррей и др. М.:Мир, 1977.-290
с.
- Hooke R., Jeeves T.A. Direct Search Solution of Numerical аnd Statistical Problems. S.
Assoc. Computer. Mach. 8,1962, pp.212- 229.
- Nelder J.A., Mead R. Computer J., 7, 1964, pp.368.
- Rosenbrok H.H. Computer J., 3,1960, pp.175.
- Powell M.J.D. Computer J., 7,1964, pp.155; 7,1965, pp.303.
- Pearson J.D. Computer J., 13,1969, pp.171.
- Flatcher R., Powell M.J.D. Computer J., 6,1963, pp.163-168.
- Flatcher R., Reeves C.M. Computer J., 7,1964, pp.149.
- Полак Э. Численные методы оптимизации, Мир, 1974,
с.65
Теория нелинейного программирования
не дает ответа на вопрос о том, какие методы
лучше, а какие хуже, поэтому при выборе методов
следует руководствоваться собственным опытом
решения оптимальных задач в той или иной области
и учитывать специфику алгоритма.
Методы нулевого порядка (не
использующие частных производных целевой
функции по независимым переменным):
- Метод покоординатного спуска;
- Метод деформируемого многогранника;
- Метод Розенброка;
- Метод Пауэлла 0.
Методы первого порядка (использующие
частные производные* целевой функции по
независимым переменным):
- Метод наискорейшего спуска;
- Метод тяжелого шарика;
- Метод Флетчера-Ривса;
- Метод Полака-Рибьера;
- Проективный метод Ньютона-Рафсона;
- Метод Давидсона-Флетчера-Пауэлла;
- Метод Бройдена (ранг 1);
- Метод Пирсона 2;
- Метод Пирсона 3.
* Частные производные вычисляются
численным методом.
Метод случайного поиска: Монте-Карло.
Все алгоритмы, хотя и с разной
эффективностью, позволяют находить решение
оптимизационных задач. Разработчики
программного комплекса могут лишь посоветовать
использовать градиентные методы в тех случаях,
когда ожидаемое решение лежит далеко от
стартовой точки.
Неплохо работают методы
"наискорейшего спуска" и "тяжелого
шарика".
При уточнении решения, когда
стартовая точка находится поблизости, можно
рекомендовать метод "деформируемого
многогранника".
Еще одна рекомендация касается
использования программного комплекса на ЭВМ с
невысокой производительностью: при решении
задач с числом независимых переменных 5 и более,
лучше пользоваться методами нулевого порядка,
дабы избежать ощутимых затрат на вычисление
частных производных.
Метод "Монте-Карло"
рекомендуется использовать на
производительных ЭВМ, при проведении
предварительных исследований. Причем
целесообразно задавать большой ресурс
итераций (500-800), и задачу оптимизации ставить с
большим числом независимых переменных.
Последующий анализ протокола оптимального
поиска может навести на интересные решения в
разных частях области определения (могут быть
отслежены локальные оптимумы, которые можно
затем использовать в качестве стартовых точек
для других процедур).
Большинство поисковых методов
используют процедуру отыскания минимума функции
одной переменной. Эта процедура, в процессе
работы делает "шаги" по аргументам или в
направлении градиента, размер этих шагов
вычисляется автоматически, направление шагов
определяется алгоритмом поиска. Библиотека
программы ДИЗЕЛЬ-РК содержит 4 известных
процедуры одномерной минимизации:
- Метод квадратичной аппроксимации;
- Метод квадратичной аппроксимации с
локализацией точки минимума;
- Метод Фибоначчи;
- Метод золотого сечения.
Использование программы
оптимизации особенно эффективно при решении
задач форсирования двигателей, при разработке
новых конструкций, а также при проведении
модернизации направленной на снижение расхода
топлива и эмиссии вредных веществ.
Пример использования механизма
оптимизации приведен в статье: Многопараметрическая
оптимизация параметров среднеоборотного
судового дизеля при его форсировании на 25%.
СКАНИРОВАНИЕ
Если задача оптимизации
какого-либо процесса может быть сформулирована
как двумерная (число независимых переменных
равно двум), то для решения такой задачи
целесообразно использовать аппарат
сканирования. Возможность наглядного
графического отображения целевой функции и
ограничений сразу от двух аргументов помогает
лучше осмыслить количественные закономерности
происходящих процессов и принять оптимальное
решение.
Пример отображения результатов
сканирования в виде 3D графика и семейств
изолиний:
Влияние угла окончания выпуска и угла начала
впуска на коэффициент наполнения Eta_v и удельный
эффективный расход топлива SFC 4 тактного дизеля.
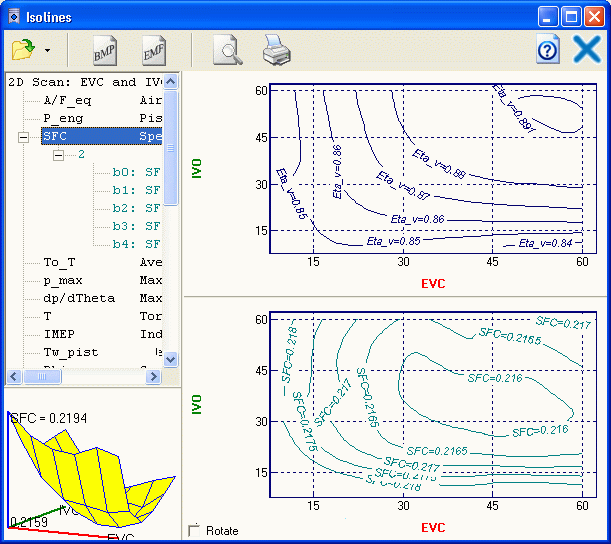
Пример отображения результатов того
же сканирования в виде укрупненного 3D графика
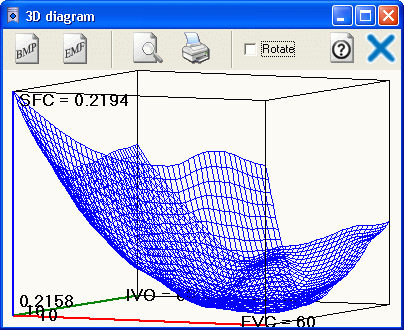
Использование аппарата
сканирования позволяет быстро находить
эффективные решения при доводке рабочего
процесса двигателей.
Вернуться на Главную страницу






|




